加密文件 (如何加密文件？介绍文件加密的简单方法)

一、文件加密的重要性

在当今时代，信息成为企业和个人的核心资产。无论是商业机密、个人隐私还是敏感数据，其安全性都非常重要。但是，随着网络攻击手段的不断更新，数据泄露事件频繁发生，如何确保文件数据安全已成为一个非常严峻的问题。文件加密作为一种有效的数据保护措施，其重要性不言而喻。

加密后的文件内容将被转换成无法直接阅读的代码形式，即使文件被非法获取，攻击者也无法轻易读取其中的内容，有效保护了信息的机密性。同时，加密技术还能防止数据在传输或存储过程中被篡改，维护了数据的完整性和真实性。此外，在数据保护法规日益严格的今天，加密文件也是符合法律要求的做法，有助于企业或个人避免因数据泄露而面临的法律风险。

二、文件加密的方法

文件加密的方法多种多样，既有简单易行的，也有技术复杂的。以下是几种常见的文件加密方法：

1.压缩加密：这种方法适用于需要压缩文件并同时加密的情况。用户只需右键单击目标文件，选择“添加到压缩包”，在新窗口中输入加密密码即可。之后，访问压缩包里的文件或解压都需要密码。

2.操作系统自带功能：一些操作系统自带了文件加密功能，用户可以通过磁盘管理功能创建一个虚拟硬盘，并将其加密。之后，将需要加密的文件拷贝到虚拟硬盘中，即可实现文件加密。

3.文件加密软件：这是最简单也是最常用的方法之一。用户只需在搜索引擎中输入“文件加密软件”，即可找到多款加密工具。这些工具通常具有友好的用户界面，用户只需几步操作即可完成文件加密。

三、安企神软件文件加密系统的优势

在众多文件加密软件中，安企神软件以其卓越的性能和全面的功能脱颖而出。

1.高强度加密：安企神软件采用AES-256位加密算法，对各类文件进行高强度加密，确保只有授权人员可以访问。这种加密不仅适用于存储在本地硬盘的文件，还适用于在移动设备和传输过程中的文件。

2.细粒度权限管理：安企神软件支持对文件进行细粒度的权限设置，包括查看、编辑、打印和分享权限。通过灵活的权限管理，企业可以有效控制内部和外部用户对敏感信息的访问。

3.多平台支持：安企神软件支持Windows、macOS、Linux等操作系统，适应企业多平台办公需求。

4.实时审计功能：安企神软件提供实时审计功能，记录所有文件的访问和操作记录，有助于提高数据追踪能力和合规性审查。

综上所述，文件加密是保护数据安全的重要手段之一。而选择一款功能强大、操作简便的加密软件，如安企神软件，更是确保数据安全的关键。

安企神文件加密系统采用高性能透明加密内核技术，是一个从源头上保障企业数据安全的安全管理系统。

透明加解密技术：当使用者在打开或编辑指定文件时，系统将自动对未加密的文件进行加密，对已加密的文件自动解密。文件在硬盘上是密文，在内存中是明文。一旦离开使用环境，由于应用程序无法得到自动解密的服务而无法打开，从而起来保护文件内容的效果。

安企神文件加密系统功能介绍

一、透明无感知加密

实行透明无感知加密，对重要文件自动进行加密，对员工正常工作不产生任何影响， 不改变用户习惯，加密文件离开公司无法打开。

1.强制加密：管理员指定类型的文件会被系统强制加密

2.使用方便：不改变用户使用电脑的一般习惯，不需要过多限制外发端口

3.内部无感：受保护文件不需特别处理，在企业内就可以正常交流

4.外流无效：受保护文件如果非法流出企业，无法打开或者显示乱码

二、智能半透明加密：

当用户打开加密文档编辑保存时，继续加密；

当用户打开非加密文档编辑保存时，不加密，

智能识别，智能处理。

三、水印防泄密

开启屏幕浮水印功能，可以对屏幕显示内容进行设定，打印文件会带有水印背景，并

记录相关操作。有效防止通过打印、拍照、截屏等方式泄密。

四、外发文件控制

可以对外发的文件进行权限设定，如可打开的次数、可打开时间、是否允许打印、复制、修改、删除、截屏等操作；并可以对外发电脑进行限定，防止二次转发造成泄密。

五、外发端口控制

管理所有外接设备，全面管控使用U盘、光驱光盘、手机拷贝等存在泄密风险的操作。

六、详细的日志审计

管理员通过文件操作记录预判泄密行为，事后追责和防抵赖。

通过文件操作记录，方便管理人员对具备潜在泄密风险的人员进行锁定，重点跟进这些人员的行为，事前防御泄密事件的发生。

　公司企业的机密文件泄露是一件很严重的问题，它随时会导致公司损失，所以每一家公司都应该对自己的数据信息进行相关的保密，而目前最常发生的泄密事件，就是在员工传导信息的时候泄露，那么我们应该要怎么解决呢?答案就是给文件加密，用文件夹加密软件。今天小编就来给大家详细的说说文件加密软件怎么去进行选择?

　　每一种技术都有针对的问题和适用环境。从数据安全技术的种类来说，有控制类技术、过滤类技术、加密类技术等。控制类技术和过滤类技术通常是作用于数据传输的端口和过程中，因此对具体的文档保护有一定缺陷。

　　这里比较推荐大家使用安企神软件

　　安企神主要功能

　　本地文件加密

　　对本地的文件进行加密，设置文件的访问权限：复制、打印、截屏、删除等。

　　共享文件加密

　　对共享文件进行加密，管理员设置用户的访问权限，设置可查看不可编辑、可编辑不可带走等。

　　文件权限分配

　　自定义设置指定用户对文件的操作权限,共享文件可以设置每个部门只允许查看本部门的文件。

　　记录操作行为

　　记录用户对文件的操作行为，只要是有人操作过，那么就一定会留下记录，方便我们查找。

　　分部门控制

　　根据文档流转的范围，对文档进行多部门的分级管理，确保文档在指定范围内使用。

　　日志审计

　　共享文件管理软件系统提供完备的日志管理,确保文件操作的可追溯性。

　　其次，加密软件功能是否满足公司需求， 看操作是否简单方便，以及售后服务，判断是否是一个品牌好的加密软件，售后服务是一个非常重要的考察点。有专门的技术人员、客服人员提供售后服务，选择安企神软件来保护数据安全，采用的透明加密技术，自动后台透明运行，无需改变电脑使用习惯，保存或另存为时文档即被高强度加密处理。

由于分形图形的不规则性，我们提出了一种分形数据文件加密算法，该加密算法用于数据文件加密，使非法用户很难破解，大大增强了信息的安全性。

一、分形加密算法

分形几何是非线性科学研究中十分活跃的一个分支，它的研究对象是自然界和非线性系统中出现的不光滑和不规则的几何形体。正是由于它的非线形，在密码学中就有了很好的用处，正如我们所熟悉的DES加密需要8个S盒来完成加密的非线形一样。我们拿形成维数n=3的席尔宾斯基垫片作为加密模型，则加密的结果如下所示：

详细过程为：

将密钥表示成二进制形式，并从左至右分为三组，第一组由密钥的第1～4位组成，第二组由密钥的第5-16位组成，其余的位数划人第三组。我们定义第一组为选择数据文件加密所用的模型，第二组为分形的形成维数，第三组中的各位作为控制位控制子图形的旋转，0代表子图形顺时针旋转一次，1代表顺时针旋转2次。

加密密钥为0x10034567，要加密的明文为0x12345678，那么密钥中第一组为0001，假设0001代表加密模型是席尔宾斯基垫片模型。第二组为000000000011，即形成维数为3，第三组为0100010101100111，用于控制子图形旋转。则用于加密的分形图形如图1所示。

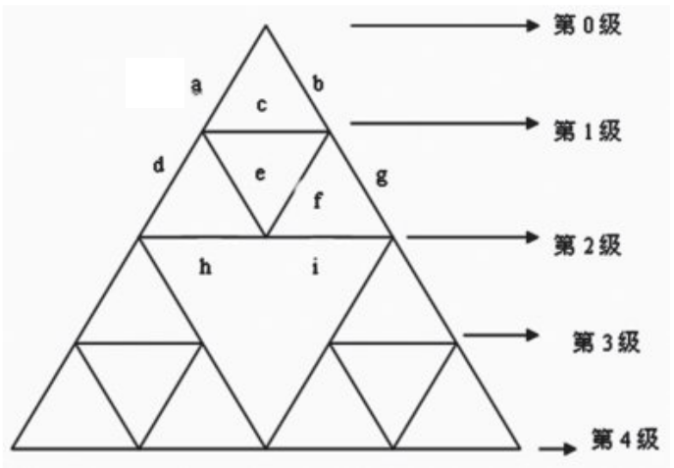
将密钥第三组填入模型中，得到密钥控制图，生成过程为：将二进制密钥第三组的每一位按照从上到下从左到右的顺序放在各顶角朝上的小三角形中，例如将上图按照每个小三角形的高的长度作为一个等级从上到下分为5级，第0级到第1级之间有一个顶角朗上的小三角形，填入密钥0，第1级到第2级之间有两个三角形，由于在同一级则按照从左到右的顺序，因此两个三角形分别填入密钥值1、0，第2级到第3级之间有两个顶角胡上的三角形，得到密钥值0、0，第3级到第4级之间有4个顶角朗上的三角形，得到密钥值为1010。生成的控制图如图2所示。

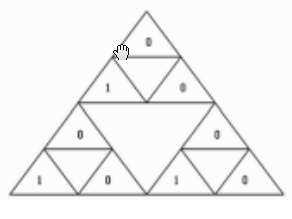
明文的二进制为0001 0010 0011 0100 0101 0110_01 11 1000，将明文填入模型中，得到明文位置图，生成过程为：将明文二进制的每一位按照从上到下从左到右的顺序放在顶角朗上的小三角形的三条边上。依然按照以上的规则将图1分为5级， 第0级和第1级之间有两条边，得到的值为00，第1级上有一条边得到的值为0，第1级到第2级之间有4条边，得到的值为1001，依此类推。生成的图形如图3所示。以下从上到下从左到右的规则都与此相同，故不再详细说明。

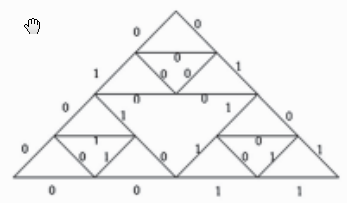
将模型中子图形按照密钥控制规则旋转，得到密钥位置图，控制规则为：在图2中如果三角形中二进制数为0的则将该三角形顺时针旋转1次，如果为1则将该三角形顺时针旋转2次。生成的密文位置图如图4所示。这样一次加密过程完成。

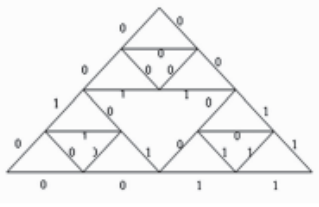
由上可知，每次加密能够加密的二进制位数为维数的三次方（如果模型为1的话），如果明文二进制位数大于一次能加密的位数，则需要继续加密，继续加密时，密钏控制位循环使用，如上次用到密钏控制位的前9位0100 0101 0，接下来使用密钏的后7位1 10 01 1 。前2位01，依此循环使用密钥，则密钏控制图如图5所示。

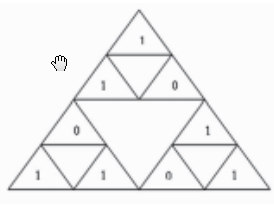
剩下明文在席尔宾斯基垫片模型中所处位置为图6所示，明文经过密钏控制后在席尔宾斯基垫片模型中的位置如图7所示。当剩下明文不足一次能加密的位数，使三角形的边上数据不够，比如图6所示，有一个三角形中只有两条边上有数据，则该三角形在加密过程中不作旋转。

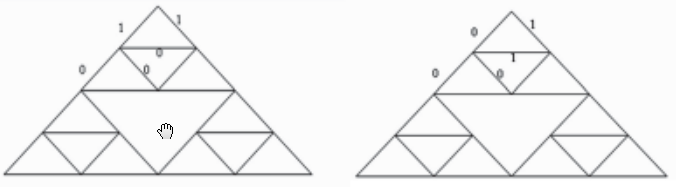
加密完成，密文按照从上到下从左到右的规则取出，得到的密文为，0000 0001 1100 1100 0010 111001 10 1 100即OxOlcc2d6c。

解密的时候0代表三角形旋转2次，1代表1次，因为三角形旋转三次就还原了，即解密过程完成，如是其他模型，加密规则同席尔宾斯基垫片模型类似。

对于所有模型有如下规则：

1）将密钥表示成二进制形式，并从左至右分为三组，第一组由密钥的第1～4位组成，第二组由密钥的第5-16位组成，其余的位数划入第三组。我们定义第一组为选择数据加密所用的模型，第二组为分形的形成维数，第三组中的各位作为控制位控制子图形的旋转。

2）设选择好的模型，当形成维数为1的时候，有m条边，如席尔宾斯基垫片模型的m值为3，席尔宾斯基地毯模型的m值为4。那么当形成维数为n时，选择子图的原则是：选择模型中与初始图形相似且在黑色区域（即不是由于形成分形图形而被挖去的部分，如下面两个图的黑色区域）的子图。该子图的个数为((m-1)2-1)n-1。如席尔宾斯基垫片模型当n=3时候的个数为9个，席尔宾斯基地毯模型当n=3时候的个数为64个。

3）旋转控制位数的确定。如席尔宾斯基垫片模型只需要一位，即0和1。但是席尔宾斯基地毯则需要两位，即00，01，1 0，1 1。因此旋转位数的选择依据为使(m--1)≤2k(k>0)成立时最小的k值，即为所需要的位数。

4）旋转次数的确定。设控制位数为k，则此时该控制位对应的十进制值为w，则加密时候旋转次数c=w%m+1，解密时旋转次数为c=m-l-w%m。

5）明文填入位置的选取准则，按照选择好的子图形中边排列的从上到下从左到右的顺序，依次填入，取出密文的时候也按照这个规则。如图1所示，填入的顺序为a，b，c，d，e，f，g，h，i等。整个加密流程图如图8所示：

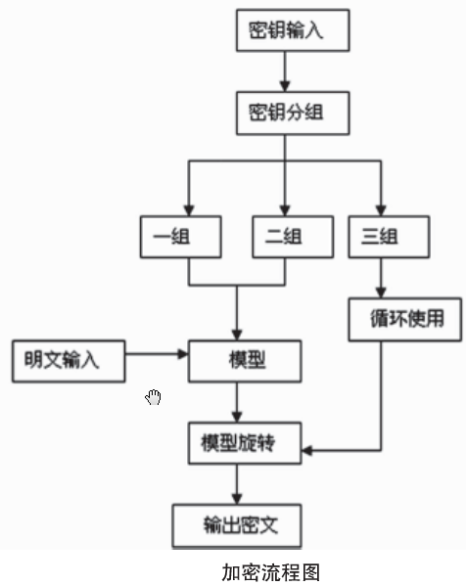
解密中明文输入部分换成密文输入，同时模型旋转次数按照规则4）中做出转化。

整个加密流程图如图8所示：

解密中明文输入部分换成密文输入，同时模型旋转次数按照规则4）中做出转化。

该加密算法在大数据文件需要加密解密的情况下使用，如网络传输数据包的加密和解密，企业中数据需要保密等，成功使用过des或3des的地方都能适用此算法。由于加密解密得到的明文密文的数据位数相同，且在拥有密钥的前提下算法可逆，因此不能用作签名算法。

二、安全性分析

该加密方法的安全性在于：

1）第1-4位选择图形，即0000 - 1111，共16种图髟可以选择，本文只介绍了最简单的子图形为三角形的模型，其它子图形如正方形，星形等，如果错误选晕图形则无法解出。

2）第5-16位为维数，过多过少的维数都会解出错误，同时维数多能够保证数据加密后密文位置具有一定的随机性，能够抵抗差分和线性攻击。

3）旋转的次数是根据密钥变化改变而改变，而且密钥循环使用，相同的明文可以加密成不同的密文，方止选择明文攻击。

4）未用到任何数学算法，因此根据数学公式无法作为破解的工具。

5）由于很好的非线形以及无规则性，很好的保护加密明文。=

6）只有穷举法才有机会攻击，而理论上穷举法对所有的加密方法都有效，但是由于密钥位数选择的任意性，因此只要密钥在8字节(64位)以上，穷举需要2的64次方次，在时间上已经是不太可能。

现在，分形理论已应用到了各个领域，人们已提出了自然分形、时间分形、空间分形、社会分形、思维分形等概念。分形理论的提出，转变了人们传统的思维方法，认识到整体与部分之间的关系可由线性进展到非线性的阶段，且它与系统论还能共同揭示整体与部分之间的多层次、多视角、多维度的关联方式。

本文运用分形图形对数据文件加密，将分形运用到密码学中，得出一种新的加密算法，并详细的分析了该算法的实现过程；而利用分形图的加密技术和解密技术，目的就是为了改变以前在信息安全技术中古板的加密方式，力求实现信息保密中的多样性，开拓分形理论的应用领域。